参考【在互联网上, 如何保密的传输信息. 小学生都懂的RSA加密算法原理.】https://www.bilibili.com/video/BV1gf4y1r75B?vd_source=10b0f5ef3c7d5760d9f6a9c8063980e6
RSA 加密算法是公钥加密算法中最著名的之一,广泛应用于数据加密和数字签名等领域。它基于大数分解的数学问题,具有较高的安全性。RSA 加密算法由 Ron Rivest、Adi Shamir 和 Leonard Adleman 在 1977 年提出,名字就是他们三个人名字的首字母。
前情概要
小红和小明是两个好朋友,他们想通过互联网互相传递消息,但是担心信息可能会被别人偷听到。他们知道,最安全的方式是对消息进行加密,但问题来了:如何安全地交换加密所需要的密钥呢?
如果他们直接交换一个密钥,坏人可能会在传输过程中窃取到这个密钥,之后就能解密所有通信内容。为了避免这种情况,小红和小明决定采用非对称加密的方法来解决密钥交换的问题。
在非对称加密中,每个人都有一对密钥:公钥和私钥。其中,公钥可以公开给任何人,而私钥则只能保存在自己手中,不可以泄露。
- 小红想要给小明发送一条加密的消息,她会用小明的公钥加密消息。
- 由于公钥是公开的,任何人都可以看到,但只有小明使用自己的私钥才能解密消息。
通过这种方式,即使坏人截获了加密的消息,也无法解密内容,因为他们没有私钥。
然而,虽然非对称加密非常安全,但它比对称加密(如AES)慢很多,特别是用于大规模数据传输时。因此,实际的通信内容通常会使用对称加密,而非对称加密则用于加密对称加密的密钥。
加密过程


欧拉函数

通信过程
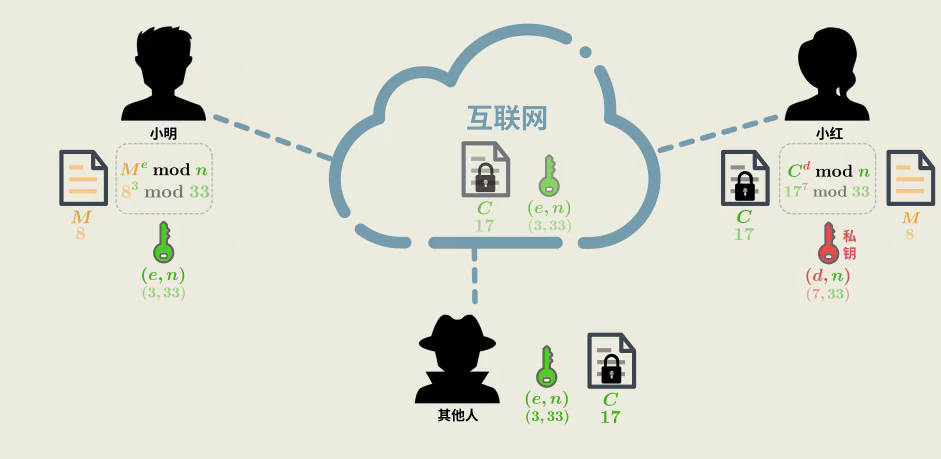
反推困难
e n C会暴露在网上,但是知道e n C并不能反推M,这是由于模运算的不可逆性

如果想通过解密公式反推出M就需要知道d值
但是大数因式分解是很困难的事情
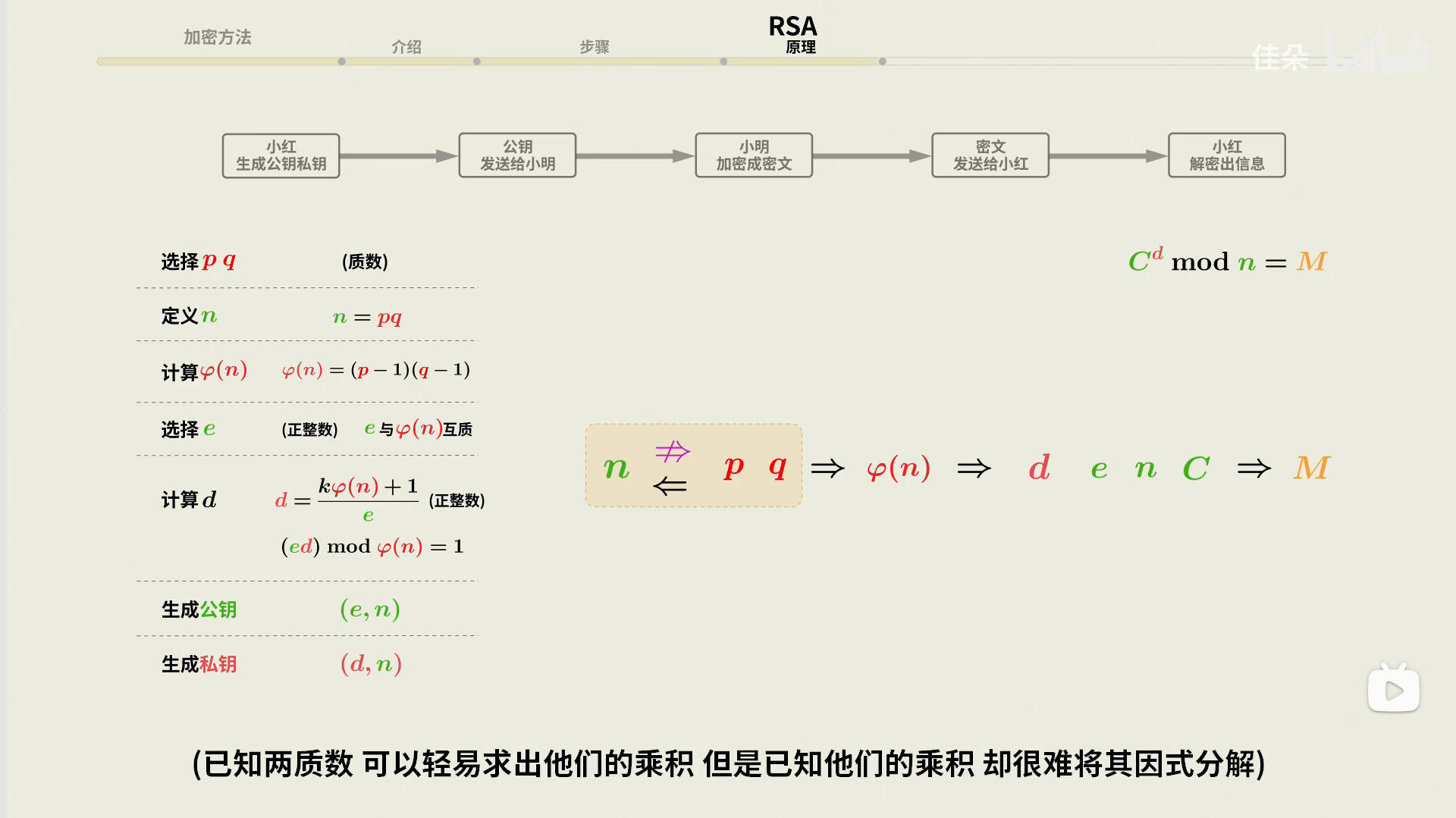
RSA与数学
RSA加密算法的安全性,主要依赖于两个数学原理:大数因式分解的困难性和模运算的不可逆性。
- 大数因式分解的困难性:RSA算法通过选择两个大素数并将它们相乘来生成公钥和私钥。尽管公钥中的大数(e和n)是公开的,但因式分解这个大数的过程极为复杂,现有的计算方法和计算能力无法在合理的时间内完成。因此,即使有人知道了公钥,也无法通过因式分解反推出私钥。
- 模运算的不可逆性:在RSA加密过程中,模运算的不可逆性是保证安全性的重要因素。RSA算法的加密过程是基于模运算(取余数)进行的,这种运算在没有私钥的情况下无法逆向操作。具体来说,虽然加密时用的是公钥和模运算,但要想从加密的消息中恢复原文,必须依赖私钥的逆运算,而这一过程是无法通过公钥简单推算出来的。
因此,RSA的安全性不仅仅依赖于大数因式分解的困难性,还因为模运算的不可逆性使得从公钥和加密内容中反推出原始信息几乎不可能。这种强大的数学保障,使得RSA算法广泛应用于数字签名和安全通信等领域。





